index

MATH2111

MATH2221

MATH2400

MATH2601

MATH2701

MATH3051

MATH3431

MATH5015

MATH5645

notes

abelianisation of a group

additive rule of probability

algebraic element

algebraic structure

all one polynomial

alternating series test

am gm inequality

any element is algebraic over field containing it

argument of complex number

arithmetic function

arithmetic mean

baby-step, giant-step

ball and sphere (metric space)

base 10 divisibility rules

basic properties of groups

behaviour of dirichlet L-function of principal character at 1

bijective function

birthday paradox

bolzano weierstrass theorem

cancelling in linear congruences

cardinality of a set

cauchy sequence

cauchy-schwarz inequality

character group

characterisation of non-unique base b expansions

characterising fields based on ideals

characters of finite group map to roots of unity

chinese remainder theorem

compactness is preserved under continuous functions

complex logarithm

composite number

composition of homomorphisms in an exact sequence

comprehension principle

concave and convex functions

conditional probability

conjugate of dirichlet character

continuity of complex component functions

continuous bijection from compact space to hausdorff space is a homeomorphism

continuous, invertible bijection which is not a homeomorphism

coprime integers

correspondence theorem

countability of a set

counting base b digits

counting solutions to quadratic equation modulo prime

de morgan's laws (set theory)

decomposition of cyclic groups

decomposition of topological space into interior, boundary and exterior

degree of field extension

degree of minimal polynomial no greater than degree of extension

degree of splitting field extension is less than factorial of polynomial degree

denominator of algebraic number

derivative of real valued complex function is zero

differentiability implies continuity

diffie-hellman key exchange protocol

dirichlet character

dirichlet L-function of principal character

dirichlet series

dirichlet's approximation theorem

discrete logarithm

discriminant of quadratic polynomial

divergence of harmonic series

divergence of the sum of reciprocals of primes

dividend in quotient module is noetherian if both the quotient and divisor are

divisibility of a square implies divisibility of the base for squarefree integers

divisor counting function

divisor counting function as convolution

efficiently calculating legendre symbols

elementary results about functions and sets

equivalent order of cosets

euclidean algorithm

euclidean metric

euler's criterion

euler's theorem

euler's totient function

event independent from itself when probability 0 or 1

every abelian group is an integer module

every field extension which is finite is algebraic

every field homomorphism is injective

every function is the sum of an even and odd function

every group of prime order is abelian

every group of prime order is cyclic

every irreducible element is prime in a unique factorisation domain

every metric space is hausdorff

every prime element is irreducible in an integral domain

every rational number is approximable to no order greater than 1

every subgroup of an abelian group is normal

existence of transcendental numbers

exploiting rsa with mersenne primes

extension field

extension field as vector space

fermat pseudoprimes

fermat's little theorem

field generated by finitely many algebraic elements is algebraic

field homomorphism

field of fractions of number ring is corresponding number field

finite and infinite sets

first isomorphism theorem (modules)

fractional ideal inverse

function composition

fundamental theorem of arithmetic

gcd property of the division algorithm

generating set of a group

glide reflection (euclidean plane)

greatest common divisor for integers

greatest common divisor from factorisation

group element to power of group order is identity

harmonic series

hausdorff space

ideal class group

ideal contains its absolute norm

ideal distributive law

identity function

image of intersection is subset of intersection of images

image of pre-image is subset of set

image of set complement

image preserves union

images preserve inclusions

independent and dependent events

infinitude of primes

integer divides sum of coprime numbers less than it

integers are countable

integers modulo prime finite field

integral basis for number field

integral formula for particular dirichlet series

integration by substitution

interchange of function and supremum

interchange of integral and discrete sum

irrationality of e

irrationality of roots of non squares

irreducibility of all one polynomial

kronecker delta

lagrange's theorem

law of total probability

lebesgue dominated convergence theorem

left and right identity are equivalent

legendre symbol

linear isometry preserves inner product

liouville's theorem

logarithm in terms of von mangoldt function

logarithm is big o of any positive power

measure of union in terms of measure of intersection

minimal polynomial (field theory)

minimal polynomial must be irreducible

minimal polynomial of algebraic integer

monotonicity and sign of derivative

multiplicative function

multiplicative group of a ring

multiplicative group of integers modulo n

multiplicativity of the legendre symbol

natural logarithm

noetherian ring

non-vanishing L(1, chi) for non-principal dirichlet character

normed vector space

order (group theory)

order of element divides order of group

orthogonality of dirichlet characters

orthogonality of group characters

partial sum of geometric series

partitioning group by cosets

permutation matrix

polar coordinates

polynomial has root if and only if it is divisible by minimal polynomial

polynomial of degree 2 or 3 over field has no roots if and only if it is irreducible

power set preserves intersection

power set sigma-algebra

powers up to order in group are distinct

pre-image preserves complement

pre-image preserves intersection

pre-image preserves union

pre-images preserve inclusions

pre-images preserve set difference

prime number theorem

primitive element theorem

probability of complementary event

probability space

probability tree diagram

product of dirichlet series

product of divisors

properties of norm of prime ideals

pythagorean triple

quadratic residue

random variable

rational integer

rational linear combinations of integral bases of number ring

rational numbers are countable

rational root lemma

rational roots of monic integer polynomials

real and complex numbers are equinumerous

real numbers are uncountable

real projective space

reflection (euclidean plane)

relationship between jacobian and complex derivative

relationship between rank, nullity, determinant and invertibility

reverse triangle inequality

ring and module homomorphisms coincide only on the identity

ring as a module over itself

ring of residue classes modulo n

ring with identity

rotation (euclidean plane)

second chebyshev function

set intersection

set is subset of pre-image of image

set of algebraic numbers is countable

short exact sequence

singular matrix

splitting function across sum with inequality given convex function

square of riemann zeta function

squarefree discriminant gives an integral basis

symmetric groups on sets of the same cardinality are isomorphic

thinking of probabilities in terms of area

tower of field extensions

transcendental element

translation (euclidean plane)

triangle inequality

uniqueness of limit of function in metric space

unit (ring theory)

unit balls in R**2

universal property of the quotient group

vector space norm

vector space of bounded linear operators

vieta's formulas

wilson's theorem

young's inequality

z is odd in any primitive pythagorean triple (x, y, z)

zero product property

Jordan Curve

Definition

Let $γ$ be a continuous path from $[a, b]$ into $C$ or $R^{2}$ such that

$γ (a) = γ (b)$
$γ (t_{1}) \neq γ (t_{2})$ for all $t_{1}, t_{2} \in [0, 1)$ satisfying $t_{1} \neq t_{2}$

Then $γ$ is called a Jordan curve.

This definition encompasses the fact that the Jordan curve sketch out a joined and closed shape in the complex plane which does not overlap itself. That is, the following is a Jordan curve

while neither of these two are

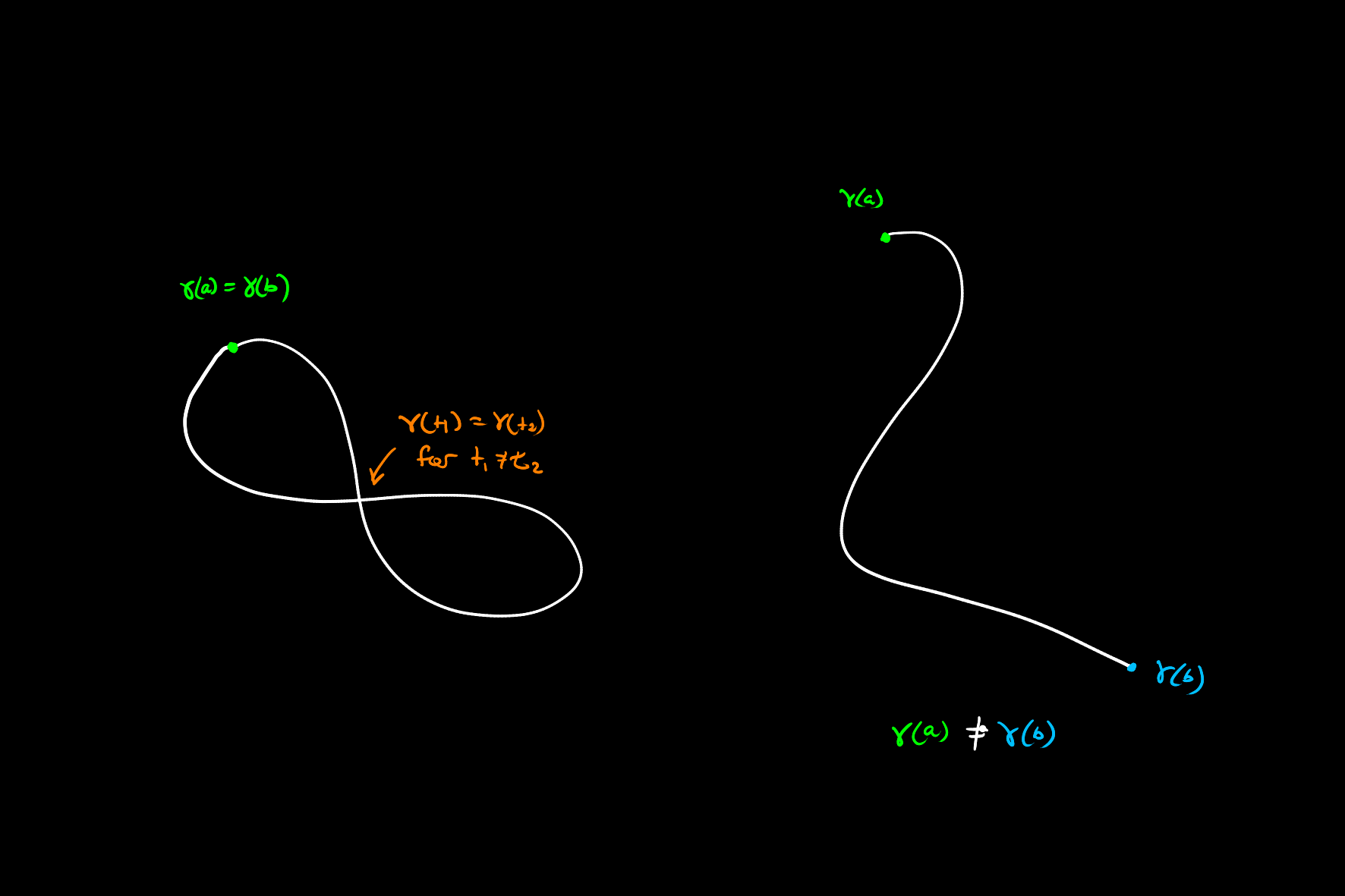
This yields a distinct inside and outside region, an idea formalised in the Jordan curve theorem.